Calculating Warren Buffett’s Rate of Return (and what you can learn from it)
- By : Menard
- Category : Investing
- Tags: Asset Classes, Compounding, Interest Rate, Warren Buffett
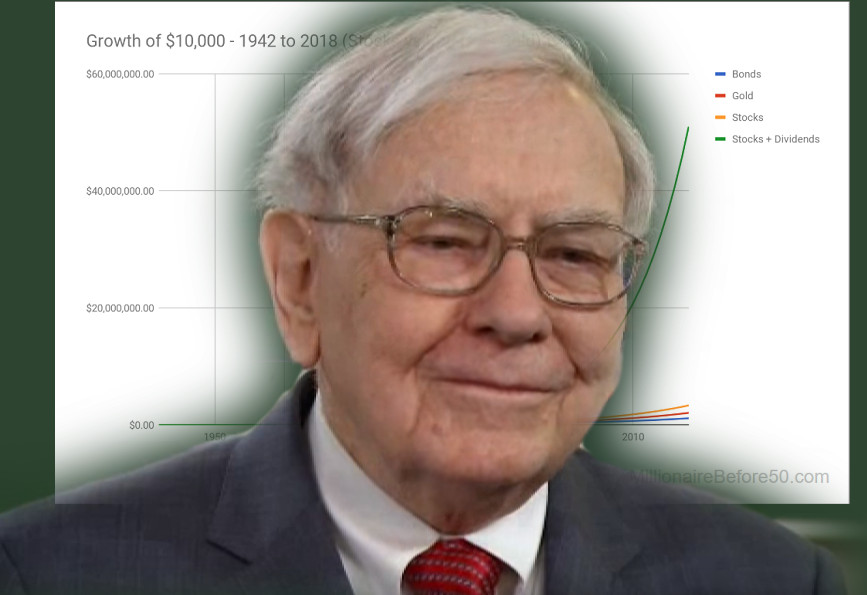
In a 2018 Berkshire Hathaway annual shareholder meeting, Warren Buffett stated that if someone invested $10,000 in a stock index fund back in 1942, it would have been worth $51 million.
An index fund is a type of mutual fund designed to match the performance of the overall market. For example, the Standard & Poor’s 500 index represents the largest 500 companies in the U.S.
Index funds weren’t available until Vanguard introduced it in 1976, but if they were, that’s how much your money would have grown, at least according to the Oracle of Omaha.
This begs the question…
What rate of return was he using in making the assertion?
I was curious to know. So I quickly googled the formula and wrote it on a piece of paper:
A = P (1 + r)t
I stared at the equation and realized that what I needed, the rate of return r, wasn’t on the left side. Bummer!
Fortunately, I still remember my high school Algebra.
This post talks about how to calculate the annualized rate of return on your investment. And while we’re at it, show you why stocks are the best place to be.

Obtaining the Annual Rate of Return
First, we need to divide both sides by the Principal. This result in P being canceled out on the right side to obtain the following equation.
(A ÷ P) = (1 + r)t
We then move exponent t, to the left side of the equation by inverting the value.
(A ÷ P) (1 ÷ t )= (1 + r)
We then move the 1 to the left by subtraction.
(A ÷ P) (1 ÷ t ) – 1 = r
Tada! We just derived the formula for the Compound Annual Growth Rate or C.A.G.R.
A stock position might be up 30% one year and down by 10% the next depending on how volatile the stock is. But the CAGR will give you the annual rate of return as if your investment had grown at a steady upward (or downward, if you are losing money) pace.
Let’s now substitute Warren’s values, taking into account that 1942 to present spans 75 years.
($51,000,000 ÷ $10,000) (1 ÷ 75 years ) – 1 = ???
No need to grab a calculator; I’ve precalculated it for you.
The answer is 11.888079147% or simply 11.89%
That’s the annual rate of return that Mr. Buffett thinks you would have made on your hypothetical investment. That assumes that you’ve reinvested the dividends, which is usually paid at a quarterly basis. That’s how much the U.S. Stock Market has performed in the last 75 years. At least, that’s what the greatest investor of all-time was implying.
“But I heard stocks are risky. What if I invested the money in Government Bonds or Gold?” You might ask.
Good thing that I stumbled upon some handy calculators at DQYDJ.com (Don’t Quit Your Day Job). I’m able to come up with historical CAGR for the other asset classes.
| Bonds | Gold | Stocks | Stocks + Dividends |
|---|---|---|---|
| 5.37% | 7.27% | 7.95% | 11.89% |
Note that these are inflation-unadjusted returns. To preserve your spending power, you need returns that far outpace the rate of inflation, which could easily be over 3% on the average. As the above table shows, stocks have delivered returns far ahead of inflation.
Especially when the dividends are reinvested…

As you can see in the above chart, the compounding effect of dividend reinvestment only gets more dramatic over time. Over the span of several decades, the choice to reinvest your dividends and simply let your investments grow could literally mean millions in additional returns.
Here are the ending values.
- Bonds, $534,249
- Gold, $2,085,060
- Stocks, $3,358,491
- Stocks + Dividends, $51,000,000
The last one wins hands down. It’s not even close.



No Comments